Here is an fun proof I saw during a stay at MSRI (Mathematical Sciences Research Institute) – unfortunately, I can not remember the reference (or none was given). If you happen to know the originator of this work, please let me know and I will attribute it appropriately. In any event, it is a “fun” problem, so I typed up the following summary:

Prop: There exists precisely one pair of numerically non-symmetric six-sided dice with no blank sides such that the sum-roll probability distribution is equivalent to normal symmetric six-sided dice. (Where by sum-roll it is meant the probability of two dice rolling a sum of x, etc.)

Proof: Let a die be represented by a Polynomial in the following fashion. Powers represent the number on a side of a die, and the coefficient of a specific power represents the number of sides with that number of dots. For example, a normal symmetric die has the following representation:

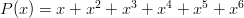
And a four sided die with three sevens and one four would be:

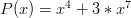
Notice that with this representation, 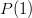is the number of sides on the die. Also notice that this representation encapsulates the probability of a specific roll, i.e., the probability of a die 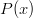rolling a “n” is:

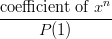
Finally, the action of rolling two dice is equivalent to forming the product of the polynomial representations. For example, when two normal symmetric six-sided dice are rolled, the probability of rolling a one (in sum) is zero, the probability of rolling a two is 1/36, the probability of rolling a seven is 1/6, etc. Notice that if we form the product

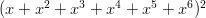
Then the coefficient of 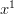is zero, the coefficient of 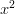is one, and the coefficient of 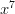is six (0/36, 1/36, and 6/36).

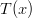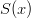Now, to answer the original question, we find two polynomials, and such that:

1)
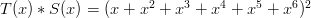
2)
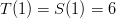
3)
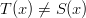
4)

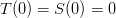
Condition #1 gives us the same sum-roll distribution as normal symmetric dice.
Condition #2 gives us two six-sided dice.
Condition #3 assures us of the non-symmetry of 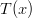and .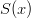
Condition #4 is equivalent to saying that the polynomials have a zero coefficient for the 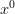term, which is the same as saying that the dice have no blank sides.

So, to proceed, we simply need to factor the polynomial in condition #1. Here it is:

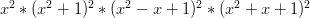
Which I’ll write as:

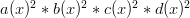
where:

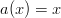
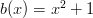
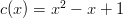
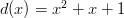
Notice that 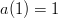so multiplying by 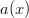will not change the number of sides on the die. Also notice that if we put both 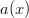terms in one of 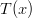or 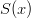then the other die would have a blank side (since the product of any of the remaining terms 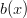, 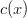or 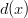would incur a monomial). Thus, both 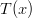and 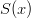must have 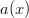as a factor.

Now, notice that 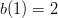and 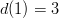, whose product is six. Also notice that 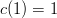. Thus, if we want 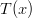and 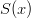to represent six-sided dice then they must both have 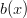and 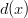as factors, since multiplying by 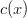will not change the number of sides. So far we have
the following:

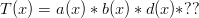
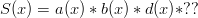
The only factor we have left is the 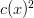. If we put a 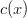in both of 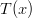and 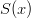then we will have created symmetric dice since 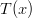will be equal to 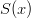(in violation of condition #3). The only other option is to put the entire 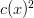term into eithe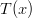r or 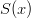By symmetry, it is irrelevant which polynomial gets the factor, so we’ll try:

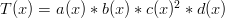
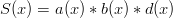
Now let’s check our work! Condition #1 is satisfied since 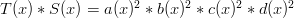. How about condition #2? Well, 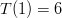and 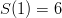so that looks good. Clearly, 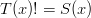so condition #3 is ok. Finally, neither term has a monic, so 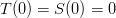and neither die has a blank side.

So, now you have all the information you need to find these dice. I didn’t want to spoil it by writing out the actual sides, so I’ll leave you the final step.